Abstract

Sharp features such as edges and corners play an important role in the perception of 3D models. In order to capture them better, we propose quadric loss, a point-surface loss function, which minimizes the quadric error between the reconstructed points and the input surface. Computation of Quadric loss is easy, efficient since the quadric matrices can be computed apriori, and is fully differentiable, making quadric loss suitable for training point and mesh based architectures. Through extensive experiments we show the merits and demerits of quadric loss. When combined with Chamfer loss, quadric loss achieves better reconstruction results as compared to any one of them or other point- surface loss functions.

Geometric Interpretation

L2 loss is a spherical loss as points equidistant from the input vertex have equal loss.
Quadric loss is an ellipsoidal loss as it penalizes displacement of points more in the normal direction.
Isoerror envelope for points on sharp features like corners is very small compared to L1 and L2, ensuring the reconstructed points to preserve such features.

Data and Code

Code

Paper

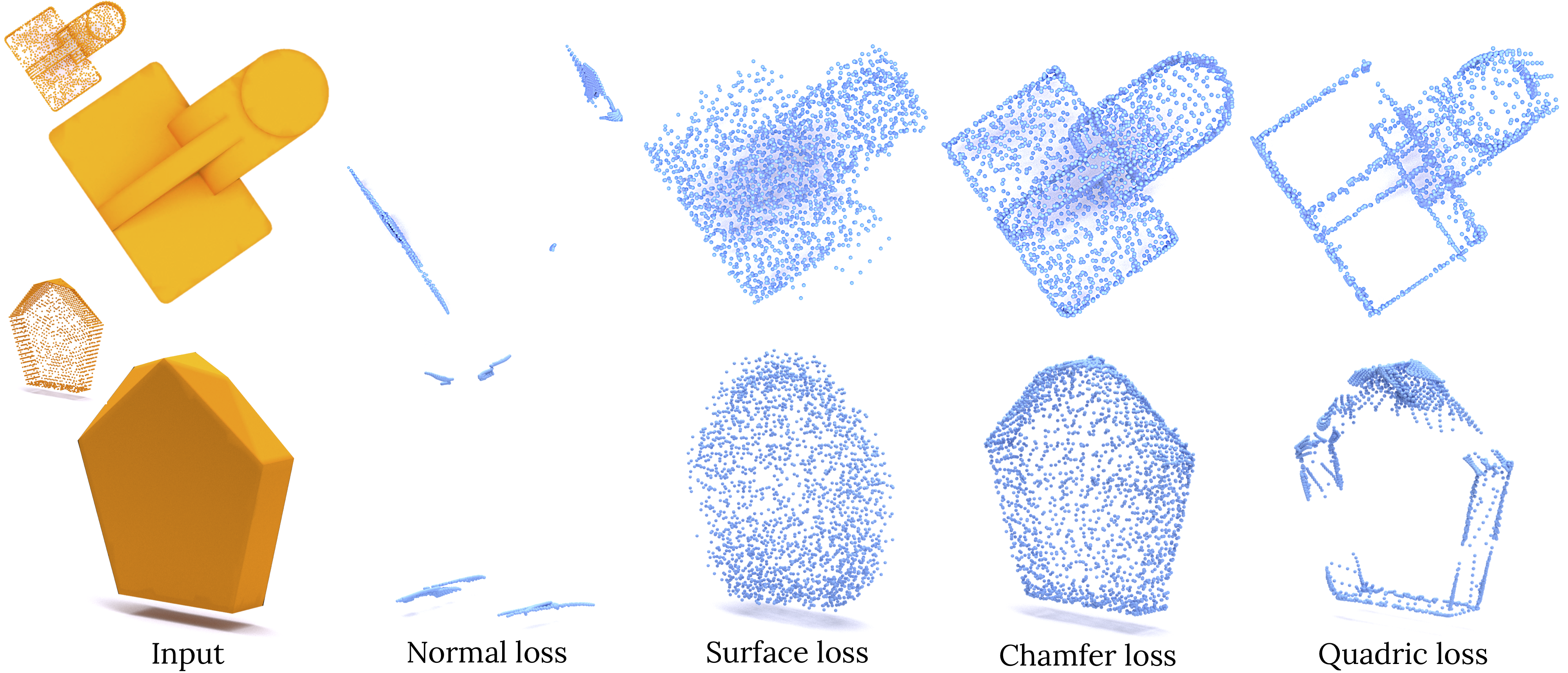
N. Agarwal, S. Yoon, M. Gopi
Learning Embedding of 3D Models with Quadric Loss
British Machine Vision Conference, 2019 [arXiv Preprint]
Supplementary Document
[Bibtex]

Few Results on ABC Dataset

Few Results on ModelNet40 Dataset

Related Work

M. Garland, P. Heckbert Surface simplification using quadric error metrics. In SIGGRAPH, 1997. [PDF]

Project template was borrowed from Richard Zhang